The MS recording technique is one of the most popular stereo microphone techniques, especially for mobile recording situations.
Its advantages are:
Disadvantage of MS technology: no spacing, i.e. no time-of-arrival differences, so the room sounds less open.
A microphone setup using the MS technique is rather easy to implement, since the two microphone housings are directed parallel to each other. For example, a double clip such as the SGMSC (HSGMSC), the AMS 22 or the stereo bar UMS 20 can be used. Even a boundary layer microphone can be expanded into an MS pair with the MS-BLM adapter. For mobile and outdoor use, an elastic suspension and windscreen are needed. There are numerous windscreens with suspensions available for MS, e.g. the basket windscreens Piano, Pianissimo and Zephyx by CINELA, or the Modular Series and the Stereo Cyclone by Rycote. These are presented in the video above.
Two microphones are used: the microphone for the mid channel M is directed forwards, while the Fig-8 microphone for the side channel S is directed with its positive lobe at -90 °.
After the general microphone equation, the two microphones can be described as follows:
M = (1-a) + a * cos (β);
S = cos (β + 90 °); where a = ball portion; β = angle of incidence;
The level at β = 0 ° is 1;
The decoding of the two signals is performed by sum and difference, wherein the proportion of Fig-8 can be set arbitrarily. The factor k (level of the S signal) determines the resulting stereo width.
L = M + k * S;
R = M - k * S; where k = level of S;
After inserting the above microphone equations into these decoding rules and some transformation operations:
L = (1-m) + m * cos (β + θ);
R = (1-m) + m * cos (β-θ); where m = omni portion; β = angle of incidence;
The resulting signals L and R thus correspond to first order microphones in a coincident arrangement, which are arranged at an angle ± θ to one another, ie at an offset angle of 2θ.
The angle θ results from θ = atan (k / a) -> the more S is mixed, the larger the opening angle.
The level p on the main axis of the virtual microphone is given by p = (1-a) + √ (k² + a²); -> the more S mixed, the greater the level.
The pressure gradient component m of the resulting virtual microphone results from m = √ (k² + a²) / p -> the more Fig-8 is mixed, the greater the pressure gradient component.
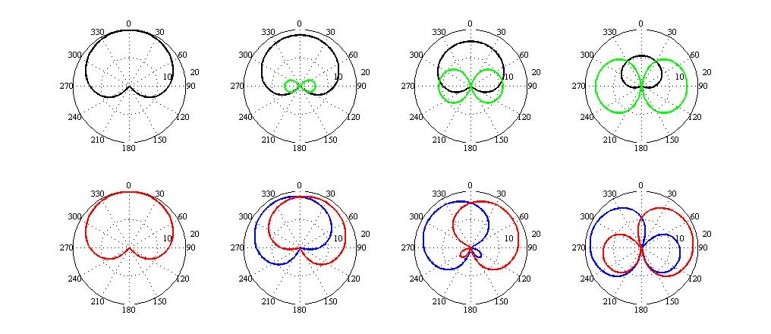
The following graphic illustrates the signals M and S (black and green), which become respectively L and R (blue and red), at different k values (levels of S):
